轨迹规划 | 图解模型预测控制MPC算法(附ROS C++/Python/Matlab仿真)

目录

• 0 专栏介绍
• 1 模型预测控制原理
• 2 差速模型运动学
• 3 基于差速模型的MPC控制
• 4 仿真实现
• • 4.1 ROS C++实现
  • 4.2 Python实现
  • 4.3 Matlab实现

0 专栏介绍

🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备！详细介绍全局规划(图搜索、采样法、智能算法等)；局部规划(DWA、APF等)；曲线优化(贝塞尔曲线、B样条曲线等)。

🚀详情：图解自动驾驶中的运动规划(Motion Planning)，附几十种规划算法

---

1 模型预测控制原理

模型预测控制(Model Predictive Control，MPC)是一种先进的控制策略，广泛应用于工程领域。它通过建立动态系统的数学模型，并基于当前状态进行预测，优化未来一段时间内的控制动作，以达到最优的控制效果。模型预测控制通过预测和优化方法，能够在系统动态变化和约束条件下，实现更高效、更灵活的控制，因此在工业应用中具有重要的实际价值。

形式化地，以下图阐述模型预测控制原理。不计较模型形式，以状态空间模型为例

$$\{\begin{array}{l}\mathbf{x}\left(k+1\right)=\mathbf{f}\left(\mathbf{x}\left(k\right),\mathbf{u}\left(k\right)\right),\mathbf{x}\left(0\right)={\mathbf{x}}_0\\ \mathbf{y}\left(k\right)=\mathbf{h}\left(\mathbf{x}\left(k\right),\mathbf{u}\left(k\right)\right)\end{array}$$

其中$\mathbf{x}\left(k\right)\in {\mathbb{R}}^n$、$\mathbf{u}\left(k\right)\in {\mathbb{R}}^l$、$\mathbf{y}\left(k\right)\in {\mathbb{R}}^q$分别表示时刻 系统的状态、控制输入和输出向量。基于预测模型可以计算预测方程，根据预测方程可以求解系统起始于$\mathbf{y}\left(k\right)$的未来一段时间内的输出序列

$$\left\{{\mathbf{y}}_p\left(k+1|k\right),{\mathbf{y}}_p\left(k+2|k\right),\cdots ,\mathbf{y}\left(k+p|k\right)\right\}$$

其中$p$称为预测时域

控制输入序列

U k = d e f { u ( k ∣ k ) , u ( k + 1 ∣ k ) , ⋯   , u ( k + p − 1 ∣ k ) } U_k\xlongequal{\mathrm{def}}\left\{ \boldsymbol{u}\left( k|k \right) , \boldsymbol{u}\left( k+1|k \right) , \cdots , \boldsymbol{u}\left( k+p-1|k \right) \right\} Uk​def {u(k∣k),u(k+1∣k),⋯,u(k+p−1∣k)}

是MPC需要求解的优化问题的独立变量。最常见的，我们希望系统实际输出 跟踪期望的参考输入

{ r ( k + 1 ) , r ( k + 2 ) , ⋯   , r ( k + p ) } \left\{ \boldsymbol{r}\left( k+1 \right) , \boldsymbol{r}\left( k+2 \right) , \cdots , \boldsymbol{r}\left( k+p \right) \right\} {r(k+1),r(k+2),⋯,r(k+p)}

同时满足实际问题的约束条件，例如控制约束和输出约束

$$\{\begin{array}{l}{\mathbf{u}}_{\min }⩽\mathbf{u}\left(k+i\right)⩽{\mathbf{u}}_{\max },i⩾0\\ {\mathbf{y}}_{\min }⩽\mathbf{y}\left(k+i\right)⩽{\mathbf{y}}_{\max },i⩾0\end{array}$$

根据这些指标设计优化目标函数$J=J\left(y\left(k\right),U_k\right)$，其最优解可记为

$$U_k^{\ast }=\arg \underset{U_k}{\min }J\left(y\left(k\right),U_k\right)$$

将$k$时刻优化解$U_k^{\ast }$的第一个分量实际作用于系统，并在$k+1$时刻以新得到的测量值$y(k+1)$为初始条件重新预测系统未来输出并求解优化问题。随着当前时间向前推移，预测时域也向前滚动

2 差速模型运动学

根据差分机器人运动学模型

$$\dot{\mathbf{p}}=\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right]=\left[\begin{array}{c}v\cos \theta \\ v\sin \theta \\ \omega \end{array}\right]=\left[\begin{array}{c}{f}_1\\ f_2\\ f_3\end{array}\right]$$

选择状态量$\mathbf{p}={\left[\begin{array}{ccc}x& y& \theta \end{array}\right]}^T$和状态误差量$\mathbf{x}={\left[\begin{array}{ccc}x-x_r& y-y_r& \theta -{\theta }_r\end{array}\right]}^T$，控制量$\mathbf{s}={\left[\begin{array}{cc}v& \omega \end{array}\right]}^T$和控制误差量$\mathbf{u}={\left[\begin{array}{cc}v-v_r& \omega -{\omega }_r\end{array}\right]}^T$，可得

$$\mathbf{x}\left(k+1\right)=\left(T\mathbf{A}+\mathbf{I}\right)\mathbf{x}\left(k\right)+T\mathbf{Bu}\left(k\right)$$

其中

$$\mathbf{A}=\left[\begin{array}{ccc}0& 0& -v_r\sin {\theta }_r\\ 0& 0& v_r\cos {\theta }_r\\ 0& 0& 0\end{array}\right],\mathbf{B}=\left[\begin{array}{cc}\cos {\theta }_r& 0\\ \sin {\theta }_r& 0\\ 0& 1\end{array}\right]$$

定义输出方程

$$\mathbf{y}\left(k\right)=\mathbf{C}\left(k\right)\mathbf{x}\left(k\right)$$

其中$\mathbf{C}\left(k\right)$定义为单位阵

3 基于差速模型的MPC控制

为了引入模型预测控制，设计状态向量

$$\tilde{\mathbf{x}}\left(k\right)=\left[\begin{array}{c}\mathbf{x}\left(k\right)\\ \mathbf{u}\left(k-1\right)\end{array}\right]$$

则

$$\tilde{\mathbf{x}}\left(k+1\right)=\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ 0& {\mathbf{I}}_{N_u}\end{array}\right]\tilde{\mathbf{x}}\left(k\right)+\left[\begin{array}{c}\mathbf{B}\\ {\mathbf{I}}_{N_u}\end{array}\right]\Delta \mathbf{u}\left(k\right)$$

接着基于模型进行系统未来动态的预测

$$\{\begin{array}{l}\tilde{\mathbf{x}}\left(k+m\right)={\tilde{\mathbf{A}}}^m\tilde{\mathbf{x}}\left(k\right)+{\sum }_{i=0}^{m-1}{\tilde{\mathbf{A}}}^i\tilde{\mathbf{B}}\Delta \mathbf{u}\left(k+m-1-i\right)\\ \tilde{\mathbf{x}}\left(k+p\right)={\tilde{\mathbf{A}}}^p\tilde{\mathbf{x}}\left(k\right)+{\sum }_{i=p-m}^{p-1}{\tilde{\mathbf{A}}}^i\tilde{\mathbf{B}}\Delta \mathbf{u}\left(k+p-1-i\right)\end{array}$$

同理，可迭代计算系统输出

$$\{\begin{array}{l}\tilde{\mathbf{y}}\left(k+m\right)={\tilde{\mathbf{C}}\tilde{\mathbf{A}}}^i\tilde{\mathbf{x}}\left(k\right)+{\sum }_{i=0}^{m-1}{\tilde{\mathbf{C}}\tilde{\mathbf{A}}}^i\tilde{\mathbf{B}}\Delta \mathbf{u}\left(k+m-1-i\right)\\ \tilde{\mathbf{y}}\left(k+p\right)={\tilde{\mathbf{C}}\mathbf{A}}^i\tilde{\mathbf{x}}\left(k\right)+{\sum }_{i=p-m}^{p-1}{\tilde{\mathbf{C}}\tilde{\mathbf{A}}}^i\tilde{\mathbf{B}}\Delta \mathbf{u}\left(k+p-1-i\right)\end{array}$$

定义预测输出向量和控制输入向量为

$${\mathbf{Y}}_p\left(k\right)\stackrel{\mathrm{def}}{=}{\left[\begin{array}{c}\tilde{\mathbf{y}}\left(k+1\right)\\ \tilde{\mathbf{y}}\left(k+2\right)\\ ⋮\\ \tilde{\mathbf{y}}\left(k+p\right)\end{array}\right]}_{p\times 1},\Delta {\mathbf{U}}_m\left(k\right)\stackrel{\mathrm{def}}{=}{\left[\begin{array}{c}\Delta \mathbf{u}\left(k\right)\\ \Delta \mathbf{u}\left(k+1\right)\\ ⋮\\ \Delta \mathbf{u}\left(k+m-1\right)\end{array}\right]}_{m\times 1}$$

则系统输出方程可表达为矩阵形式

$${\mathbf{Y}}_p\left(k\right)=S_x\tilde{\mathbf{x}}\left(k\right)+S_u\Delta {\mathbf{U}}_m\left(k\right)$$

基于预测方程定义开环优化目标函数

$$J={\left({\mathbf{Y}}_p-{\mathbf{Y}}_r\right)}^T\tilde{\mathbf{Q}}\left({\mathbf{Y}}_p-{\mathbf{Y}}_r\right)+\Delta {\mathbf{U}}_m^T\tilde{\mathbf{R}}\Delta {\mathbf{U}}_m$$

对于优化问题$\Delta {\mathbf{U}}_m=\arg {\min }_{\Delta {\mathbf{U}}_m}J\left(\Delta {\mathbf{U}}_m\right)$有

$$\frac{\partial J}{\partial \Delta {\mathbf{U}}_m}=\frac{\partial }{\partial \Delta {\mathbf{U}}_m}\left[\frac{1}{2}\Delta {\mathbf{U}}_m^T\left(S_u^T\tilde{\mathbf{Q}}{S}_u+\tilde{\mathbf{R}}\right)\Delta {\mathbf{U}}_m+{\left(S_x\tilde{\mathbf{x}}-{\mathbf{Y}}_r\right)}^T\tilde{\mathbf{Q}}{S}_u\Delta {\mathbf{U}}_m\right]$$

对应转化为标准的二次规划问题

$$\Delta {\mathbf{U}}_m=\arg \underset{\Delta {\mathbf{U}}_m}{\min }\left(\frac{1}{2}\Delta {{\mathbf{U}}_m}^T\mathbf{H}\Delta {\mathbf{U}}_m+{\mathbf{g}}^T\Delta {\mathbf{U}}_m\right)$$

4 仿真实现

4.1 ROS C++实现

核心代码如下所示，采用osqp求解

Eigen::Vector2d MPCPlanner::_mpcControl(Eigen::Vector3d s, Eigen::Vector3d s_d, Eigen::Vector2d u_r,
                                        Eigen::Vector2d du_p)
{
  ...

  // Calculate kernel
  std::vector<c_float> P_data;
  std::vector<c_int> P_indices;
  std::vector<c_int> P_indptr;
  int ind_P = 0;
  for (int col = 0; col < dim_u * m_; ++col)
  {
    P_indptr.push_back(ind_P);
    for (int row = 0; row <= col; ++row)
    {
      P_data.push_back(P(row, col));
      // P_data.push_back(P(row, col) * 2.0);
      P_indices.push_back(row);
      ind_P++;
    }
  }
  P_indptr.push_back(ind_P);

  // Calculate affine constraints (4m x 2m)
  std::vector<c_float> A_data;
  std::vector<c_int> A_indices;
  std::vector<c_int> A_indptr;
  int ind_A = 0;
  A_indptr.push_back(ind_A);
  for (int j = 0; j < m_; ++j)
  {
    for (int n = 0; n < dim_u; ++n)
    {
      for (int row = dim_u * j + n; row < dim_u * m_; row += dim_u)
      {
        A_data.push_back(1.0);
        A_indices.push_back(row);
        ++ind_A;
      }
      A_data.push_back(1.0);
      A_indices.push_back(dim_u * m_ + dim_u * j + n);
      ++ind_A;
      A_indptr.push_back(ind_A);
    }
  }

  // Calculate offset
  std::vector<c_float> q_data;
  for (int row = 0; row < dim_u * m_; ++row)
  {
    q_data.push_back(q(row, 0));
  }

  // Calculate constraints
  std::vector<c_float> lower_bounds;
  std::vector<c_float> upper_bounds;
  for (int row = 0; row < 2 * dim_u * m_; row++)
  {
    lower_bounds.push_back(lower(row, 0));
    upper_bounds.push_back(upper(row, 0));
  }

  // solve
  OSQPWorkspace* work = nullptr;
  OSQPData* data = reinterpret_cast<OSQPData*>(c_malloc(sizeof(OSQPData)));
  OSQPSettings* settings = reinterpret_cast<OSQPSettings*>(c_malloc(sizeof(OSQPSettings)));
  osqp_set_default_settings(settings);
  settings->verbose = false;
  settings->warm_start = true;

  data->n = dim_u * m_;
  data->m = 2 * dim_u * m_;
  data->P = csc_matrix(data->n, data->n, P_data.size(), P_data.data(), P_indices.data(), P_indptr.data());
  data->q = q.data();
  data->A = csc_matrix(data->m, data->n, A_data.size(), A_data.data(), A_indices.data(), A_indptr.data());
  data->l = lower_bounds.data();
  data->u = upper_bounds.data();

  osqp_setup(&work, data, settings);
  osqp_solve(work);
  auto status = work->info->status_val;

  ...

  Eigen::Vector2d u(work->solution->x[0] + du_p[0] + u_r[0], regularizeAngle(work->solution->x[1] + du_p[1] + u_r[1]));

  // Cleanup
  osqp_cleanup(work);
  c_free(data->A);
  c_free(data->P);
  c_free(data);
  c_free(settings);

  return u;
}

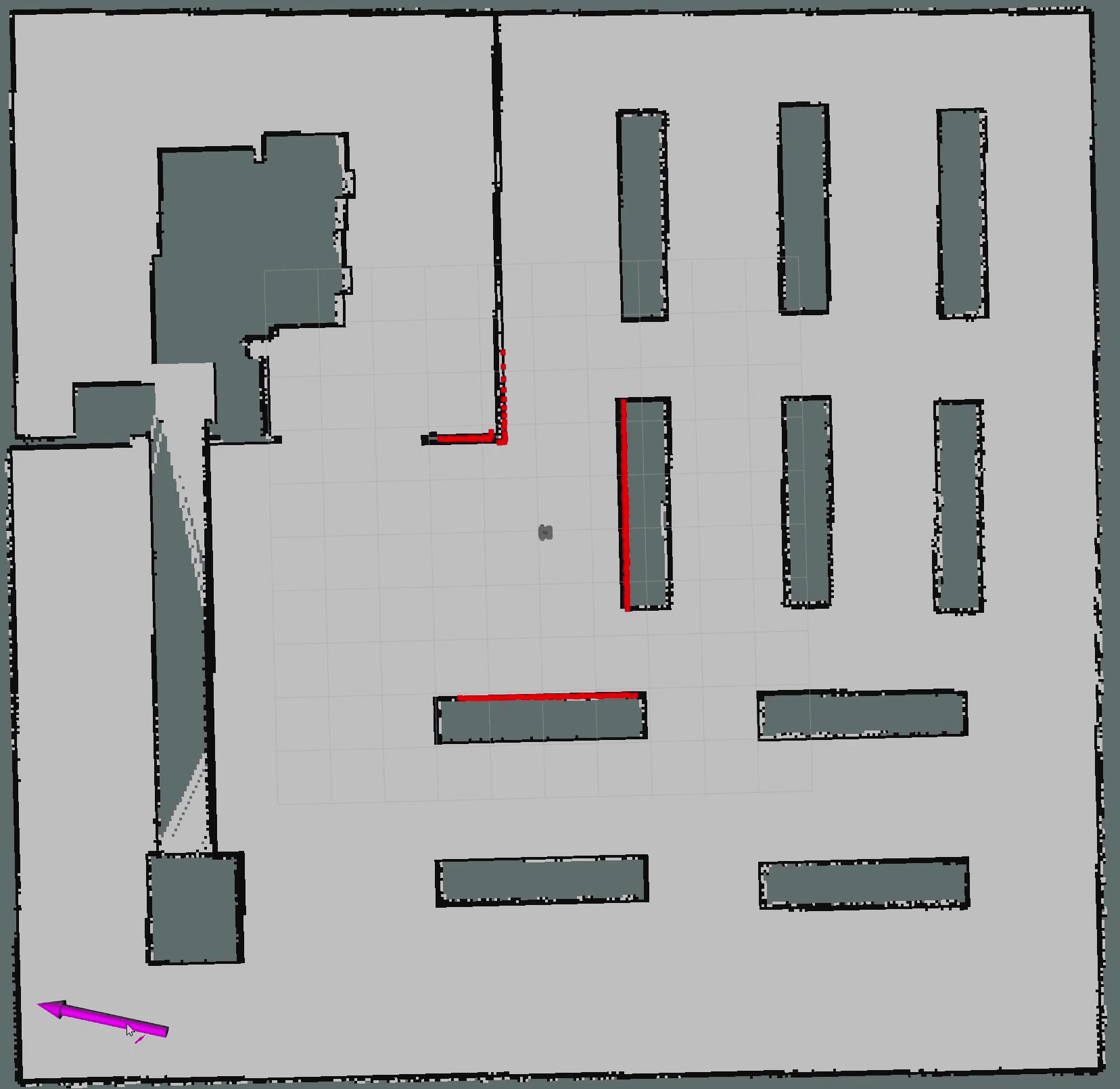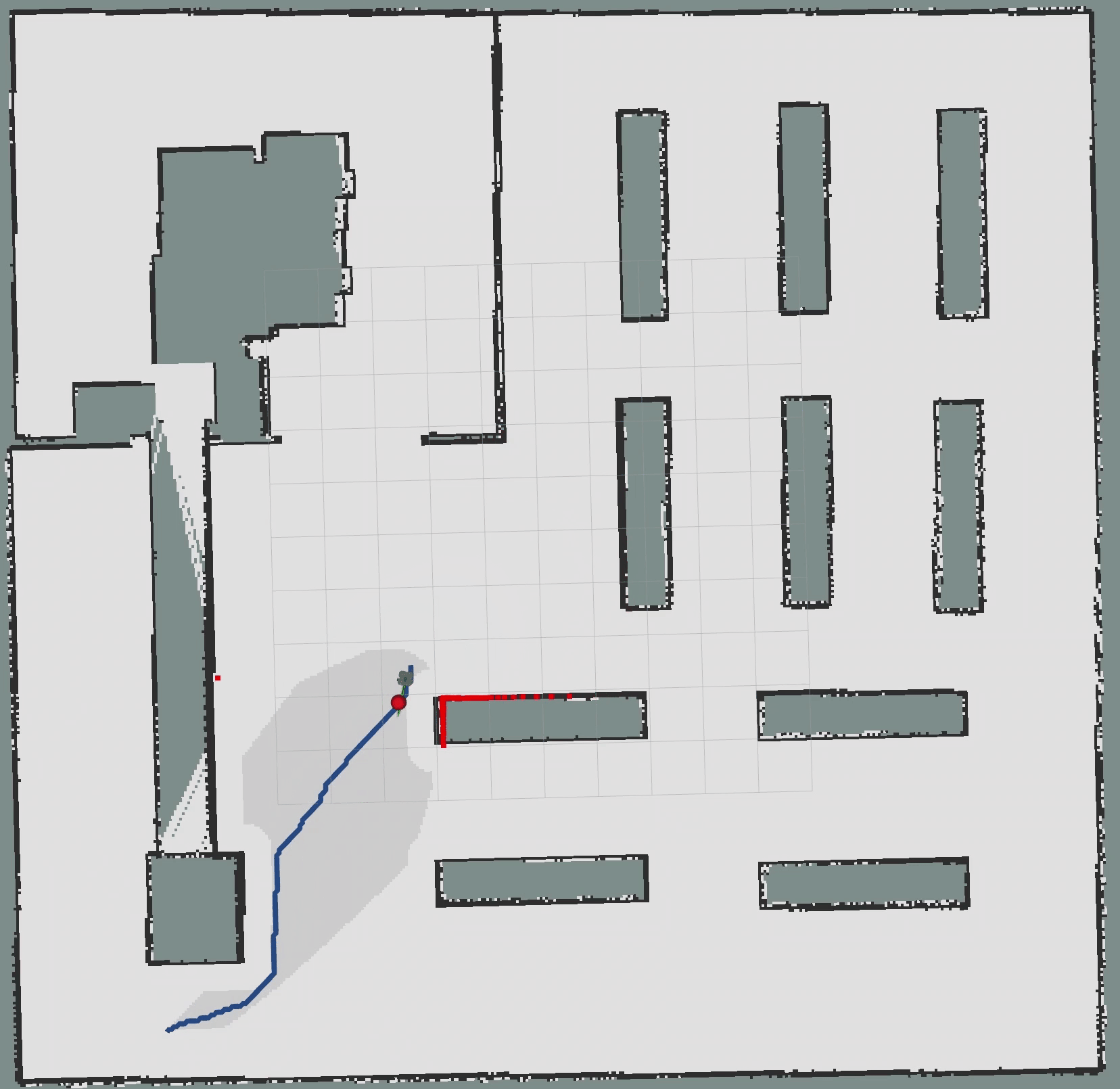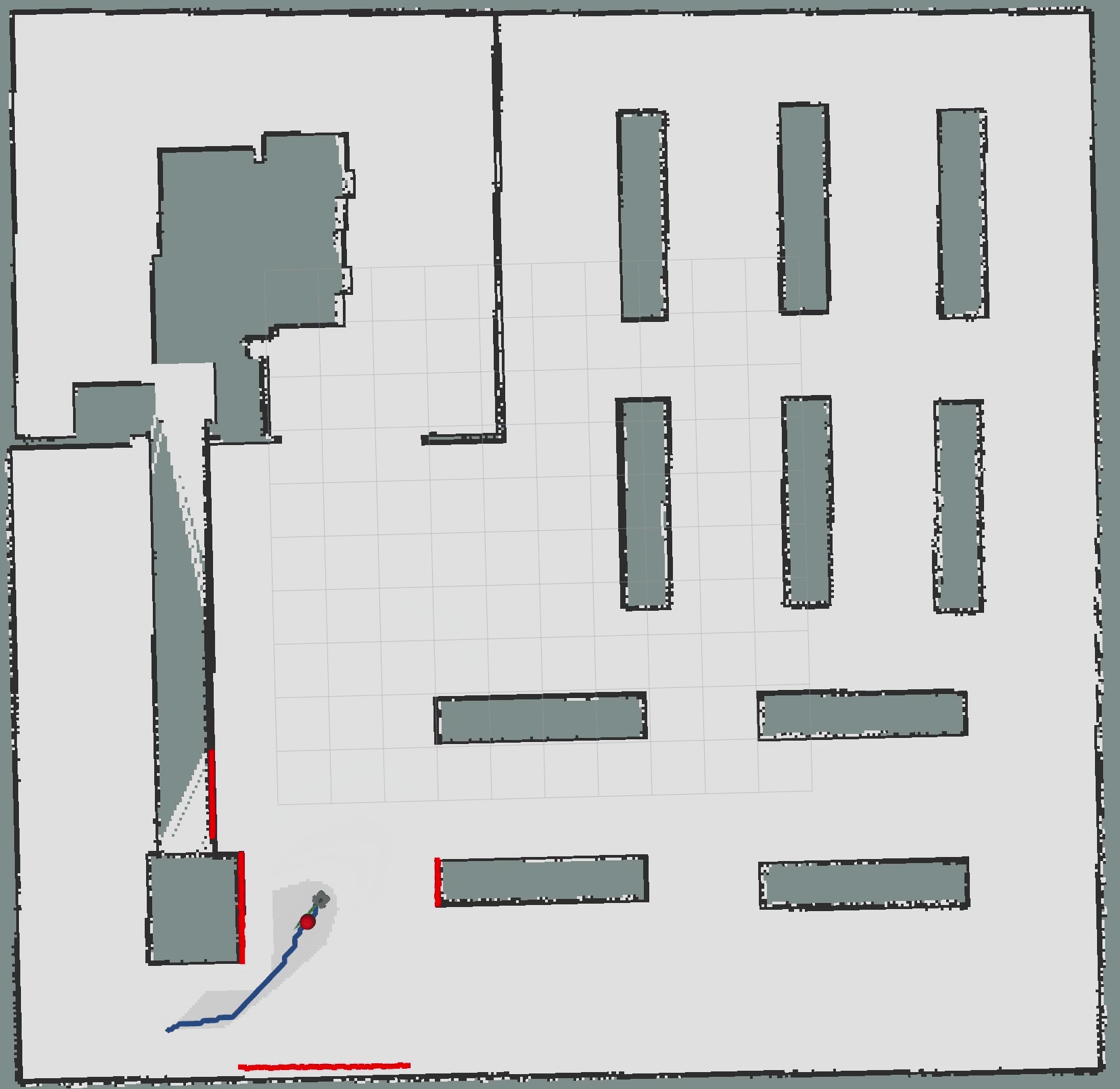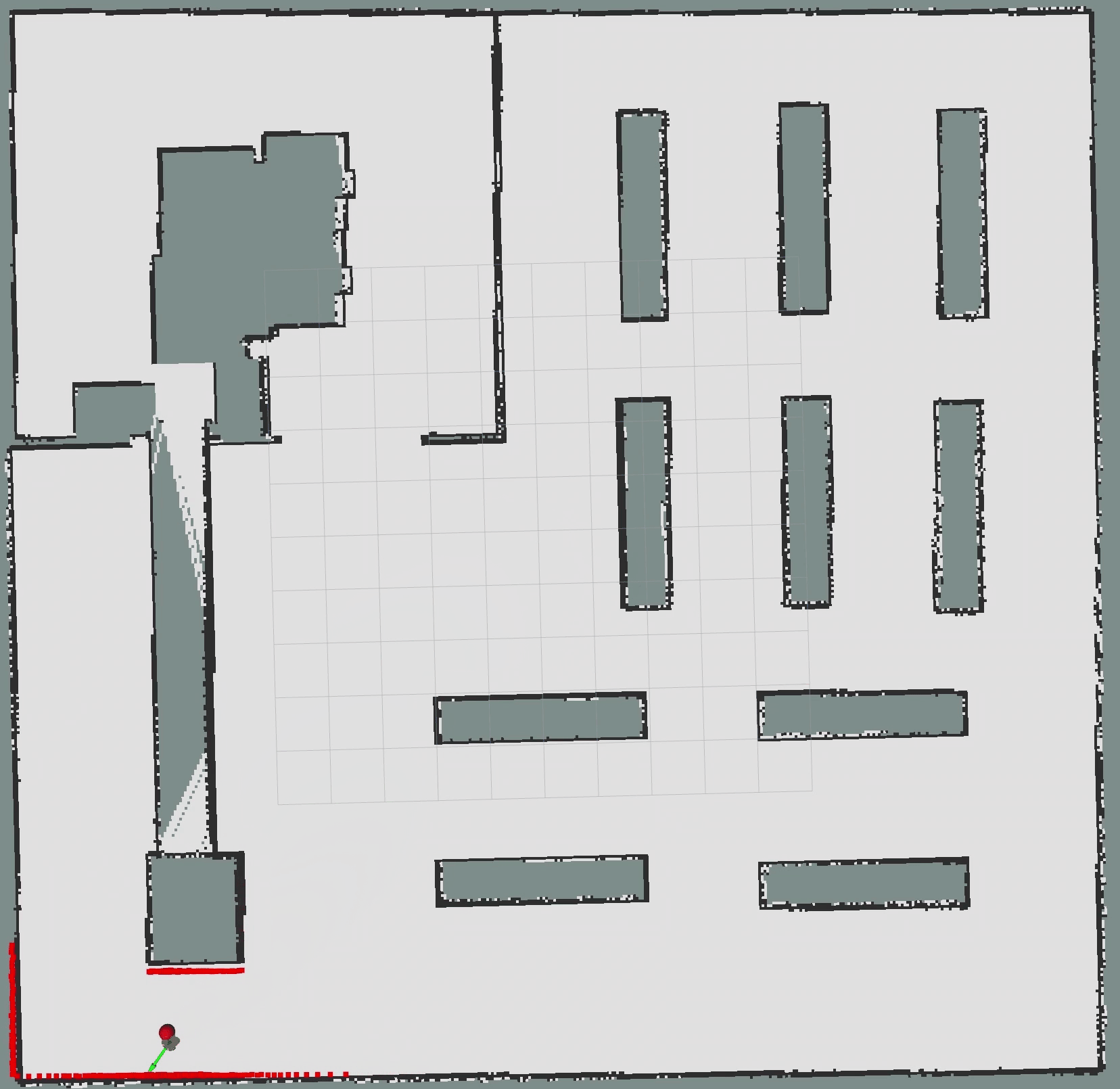
4.2 Python实现

核心代码如下所示

def mpcControl(self, s: tuple, s_d: tuple, u_r: tuple, u_p: tuple) -> np.ndarray:
	...
	
	# optimization
	Yr = np.zeros((3 * self.p, 1))              # (3p x 1)
	Q = np.kron(np.identity(self.p), self.Q)    # (3p x 3p)
	R = np.kron(np.identity(self.m), self.R)    # (2m x 2m)
	H = S_u.T @ Q @ S_u + R                     # (2m x 2m)
	g = S_u.T @ Q @ (S_x @ x - Yr)              # (2m x 1)
	
	# constriants
	I = np.eye(2 * self.m)
	A_I = np.kron(np.tril(np.ones((self.m, self.m))), np.diag([1, 1]))
	U_min = np.kron(np.ones((self.m, 1)), self.u_min)
	U_max = np.kron(np.ones((self.m, 1)), self.u_max)
	U_k_1 = np.kron(np.ones((self.m, 1)), np.array([[u_p[0]], [u_p[1]]]))
	
	# boundary
	dU_min = np.kron(np.ones((self.m, 1)), self.du_min)
	dU_max = np.kron(np.ones((self.m, 1)), self.du_max)
	
	# solve
	solver = osqp.OSQP()
	H = sparse.csc_matrix(H)
	A = sparse.csc_matrix(np.vstack([A_I, I]))
	l = np.vstack([U_min - U_k_1, dU_min])
	u = np.vstack([U_max - U_k_1, dU_max])
	solver.setup(H, g, A, l, u, verbose=False)
	res = solver.solve()
	dU_opt = res.x[:, None]
	
	# first element
	du = dU_opt[0:2]
	
	# real control
	u = du + np.array([[u_p[0]], [u_p[1]]]) + np.array([[u_r[0]], [u_r[1]]])
	
	return np.array([
	    [self.linearRegularization(float(u[0]))], 
	    [self.angularRegularization(float(u[1]))]
	]), (float(u[0]) - u_r[0], float(u[1]) - u_r[1])

4.3 Matlab实现

核心代码如下所示

function [u, u_p_new] = mpcControl(s, s_d, u_r, u_p, robot, param)
  ...
    
    % optimization
    Yr = zeros(3 * param.p, 1);                  % (3p x 1)
    Q = kron(eye(param.p), param.Q);    % (3p x 3p)
    R = kron(eye(param.m), param.R);    % (2m x 2m)
    H = S_u' * Q * S_u + R;                        % (2m x 2m)
    g = S_u' * Q * (S_x * x - Yr);                 % (2m x 1)
    
    % constriants
    A_I = kron(tril(ones(param.m, param.m)), diag([1, 1]));
    U_min = kron(ones(param.m, 1), param.u_min);
    U_max = kron(ones(param.m, 1), param.u_max);
    U_k_1 = kron(ones(param.m, 1), u_p');
    
    % boundary
    dU_min = kron(ones(param.m, 1), param.du_min);
    dU_max = kron(ones(param.m, 1), param.du_max);
    
    % solve
    options = optimoptions('quadprog', 'MaxIterations', 100, 'TolFun', 1e-16, 'Display','off');
    dU_opt = quadprog(H, g, [-A_I; A_I], [-U_min + U_k_1; U_max - U_k_1], [], [], dU_min, dU_max, [], options);
    
    % first element
    du = [dU_opt(1), dU_opt(2)];

    % real control
    u = du + u_p + u_r;
    
    u = [linearRegularization(robot, u(1), param), angularRegularization(robot, u(2), param)];
    u_p_new = u - u_r;
end

完整工程代码请联系下方博主名片获取

---

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇